前回の続きです。そちら（https://toshin-komatsu.com/452/）を読んでいない人はまずそちらからどうぞ。この記事はあくまで個人の意見なので、鵜呑みにすることはせず、参考程度にしておいてください。

定理を一度は証明しておく

　皆さんは普段、さまざまな定理や公式をつかっているでしょう。中学生の頃からお世話になっている三平方の定理、2次方程式の解の公式、それからチェバの定理、因数定理、ユークリッドの互除法、加法定理、点と直線の距離の公式、6分の1公式などなど。これらの定理の証明、一度でも見たことがありますか？

　僕は、定理の証明ができると数学の理解がぐっと深まり、数学の安定感が増すと考えています。定理や公式は、それをただ丸暗記してしまうと視野が狭くなってしまうことがあります。要は、公式を1つのパッケージをしてしか捉えておらず、まったくその通りにしかつかえない状態に陥るということです。例えば、皆さんは次の2次方程式をどのように解きますか？

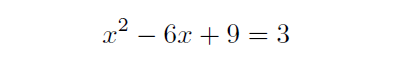
右辺の3を移項してx^2-6x+6=0の形にしてから解の公式をつかいますか？（ちなみに、x^2はxの2乗を意味します）ところで、2次方程式の解の公式は、どのように導くのだったでしょうか。その証明を知らない人は、証明しようとしてみてください。証明できる人からすれば、x^2-6x+6=0の形にすることは二度手間であるとわかります。次のようにやればよいでしょう。

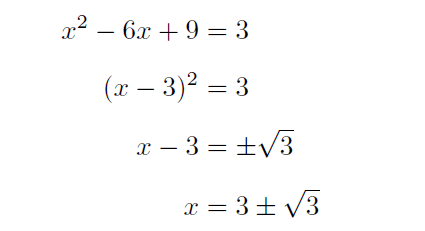
丁寧にかきましたが、実際には2行目と3行目は頭の中でやります。解の公式よりも計算強度が低いので暗算でき、計算ミスをする確率も低いです。

　このような例は他にもあるでしょう。大人でも、型にとらわれて問題が解けなくなっていることはあります。僕とて、完璧ではありません。

　公式は公式で、覚えてつかえることは重要です。僕は、1分以内に導けない公式は暗記しておけと指導します。本番は、素早く解く必要があるからです。ただし、一度はその証明をしておくようにと付け加えます。僕が高校生の頃に覚えようと思って覚えたのは加法定理と点と直線の距離の公式くらいでしょうか。逆に、1分以内に導けるものは毎回導けばよいのです。そうしているうちに勝手に覚えることは多々あります。暗記できたらラッキーくらいに思っておきましょう。ちなみに、僕は3倍角の公式が未だに覚えられません。

　それから、定理の証明ができると、定理を忘れても思い出すことができます。丸暗記している人は、忘れてしまったり細部を暗記し間違えていたりすればアウトです。初めに数学の安定感が増すと表現したのはこのことです。

　ただ証明を読むのはつまらないでしょうから、「○○の定理を示せ」と自分に問題を出してみるのはいかがでしょう。自分で証明できれば、相当えらいです。中には難しいものもありますから、そういうものは程々で諦めて教科書を見るようにしましょう。

　さて、数学の勉強の仕方を2回に渡ってかいてきました。これだけを実践すれば数学ができるようになるというものではなく、あくまで必要条件です。細かい話をしだすとキリがないので、ざっくりと3パートに分けてかきました。まだまだかきたいことはありますが、それは次回以降ということで。たまに覗いてあげてください。ではでは、よい数学ライフを！

オマケ

　公式をパッケージ化してしまうと困る例として、次のようなものを置いておきます。僕は最近、訳あって大人に出題する機会が多いのですが、そのときに正答率がよくなかったものです。理系の難関大志望の受験生ならとっておきたい問題ですね。

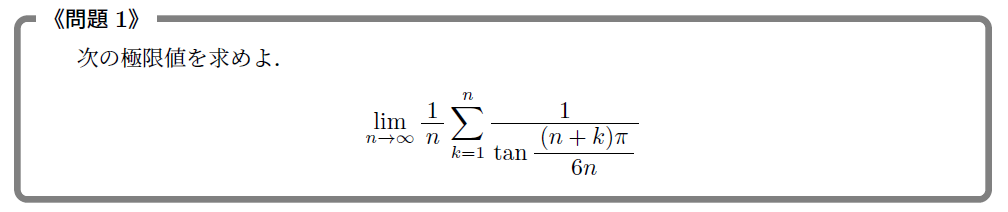
　また、次の問題は「2次方程式だ！解の公式だ！」と飛びつくとよくわからないことになる問題です。数学IIの複素数の知識があれば、文理問わず取り組めます。